5 Tests of Difference of One- and Two-sample Designs
(PSY206) Data Management and Analysis
The t-test is a statistical test used to determine whether two means differ significantly from one another.
Types of t-tests
There are three main types of t-test, each appropriate for different research designs:
- One-sample t-test – Compares the mean of a single sample against a known or expected value (e.g., a population mean).
- Independent-samples t-test – Compares the means of two independent groups (e.g., males vs. females, treatment vs. control).
- Paired-samples t-test – Compares the means from two related sets of observations, such as repeated measures on the same individuals or matched pairs.
All forms of the t-test are parametric tests, meaning they rely on certain assumptions:
- The data are measured at interval or ratio level.
- The data meet the assumption of homogeneity of variance.
- The data are drawn from a normally distributed population (see Chapter 1, Section 2).
When reporting descriptive statistics with t-test results, always provide the mean and standard deviation as measures of central tendency and variability.
In some sources, the t-test may be referred to as the Student’s t-test.
5.1 One-Sample t-Test
The one-sample t-test determines whether the mean of a sample significantly differs from a specific value.
For example, we might test whether a group’s mean performance differs from chance level, a population mean, or an expected value from previous research.
This test should only be used when the data meet the assumptions for parametric analysis.
Example Study: Assessing Memory
An enthusiastic teacher, who was also a psychology graduate, noticed that some children in her final-year primary class were frequently forgetful—forgetting lunch boxes, sports kits, or homework.
She hypothesised that these children might have poorer long-term memory compared to the population norm.
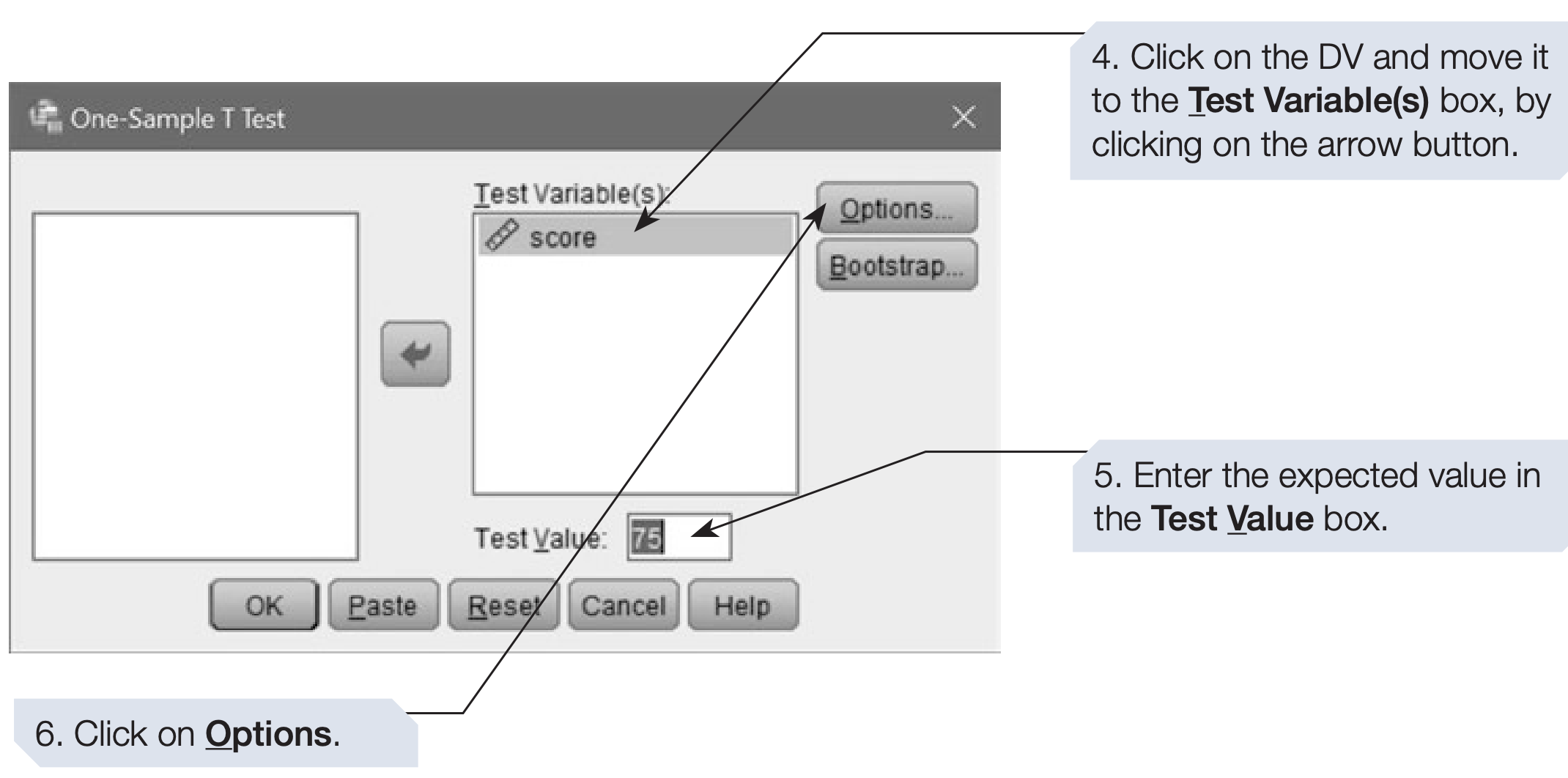
She administered a standardised long-term memory test with a published norm of 75% for children of that age. (download
score-data.xlsx)A one-sample t-test was used to test whether the class mean differed from 75%.
Performing a One-Sample t-Test
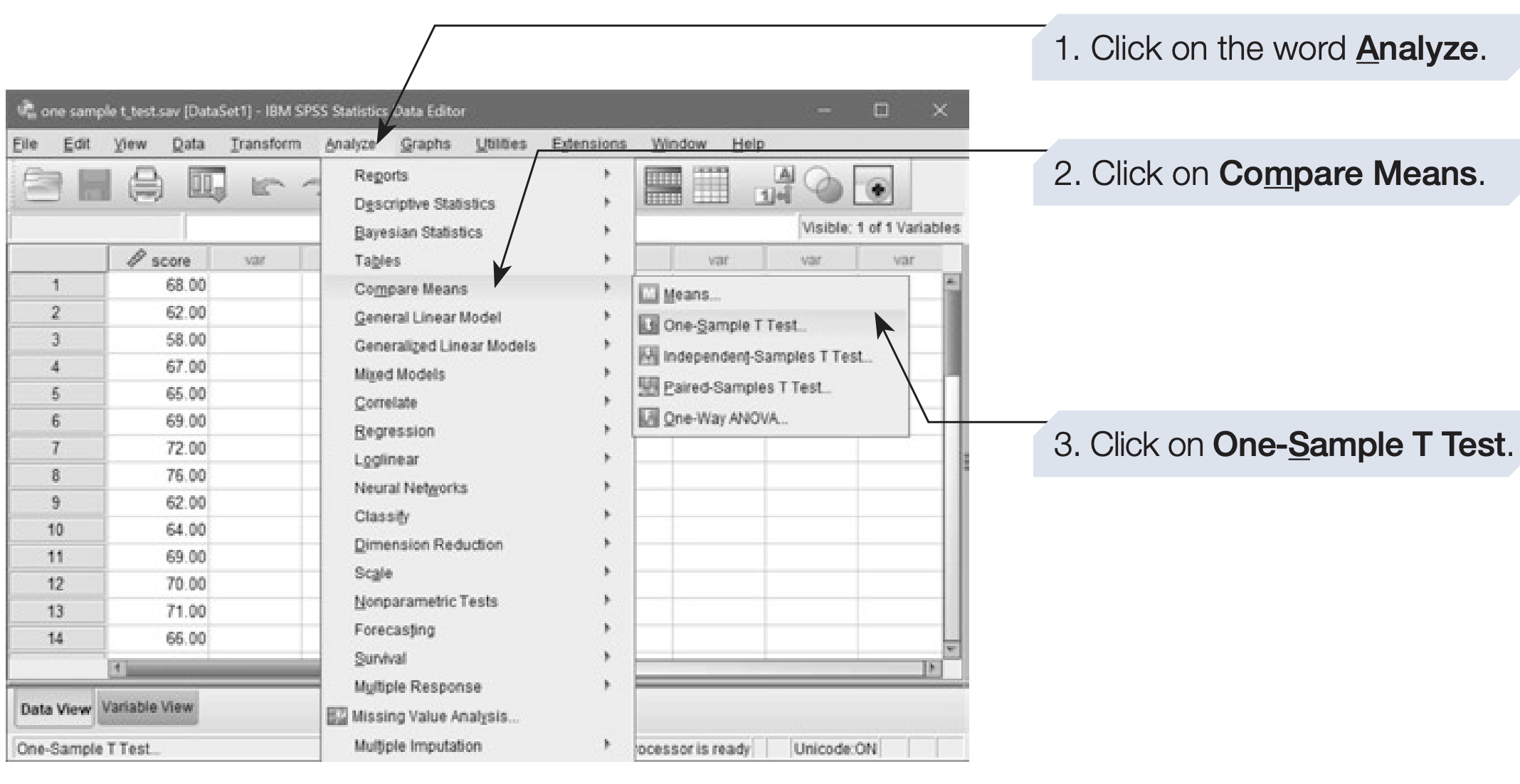
SPSS Menu Path
Analyze → Compare Means → One-Sample T Test…SPSS Syntax
T-TEST /TESTVAL = 75 /MISSING = ANALYSIS /VARIABLES = score.
SPSS Output
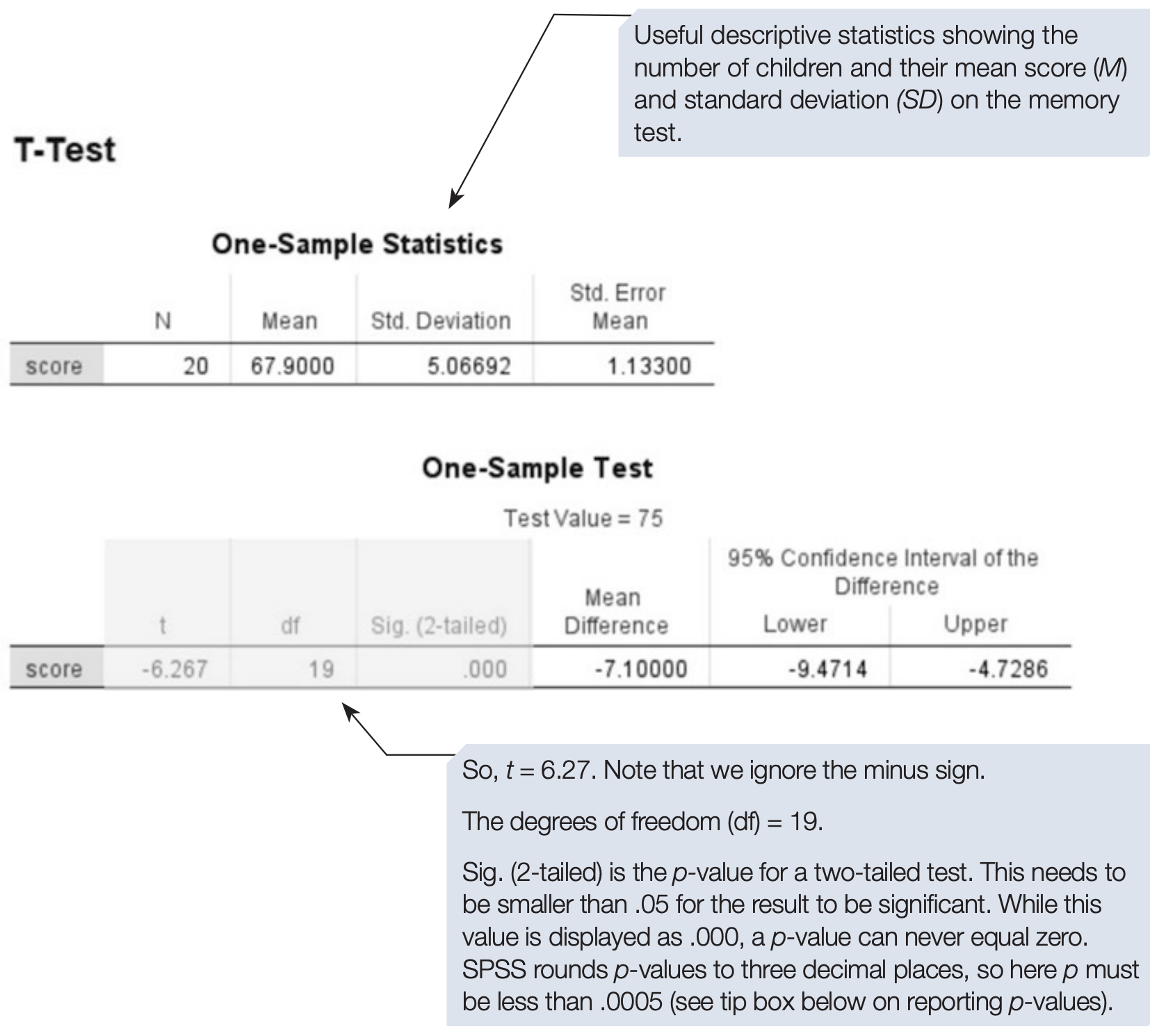
Reporting the Results
Example write-up:
Performance on a memory test by a group of forgetful children was, on average, lower (\(M = 67.9\%, SD = 5.07\)) than the expected value of 75%.
A one-sample t-test confirmed that this difference was significant (t = 6.27, df = 19, p < .001).
- Report t-statistics to two decimal places.
- Report p-values as exact values unless p < .001, in which case write p < .001.
- Do not include a leading zero before decimal values that cannot exceed 1 (e.g., p = .045, not 0.045).
5.2 Independent-Samples t-Test
- The independent t-test compares the mean performance of two independent groups.
- Use this test when the data:
- Meet parametric assumptions, and
- Come from an independent groups design (e.g., two distinct participant groups).
- Meet parametric assumptions, and
- Examples include:
- Comparing males vs. females, or
- Comparing two drug conditions (e.g., low dose vs. high dose).
- Comparing males vs. females, or
Example Study: The Memory Experiment
- In this example, we revisit the memory experiment introduced earlier (Chapter 2, download memory.sav).
- The hypothesis was that participants who received mnemonic instructions would recall more words than those who did not.
- Since the prediction is directional, a one-tailed hypothesis is used.
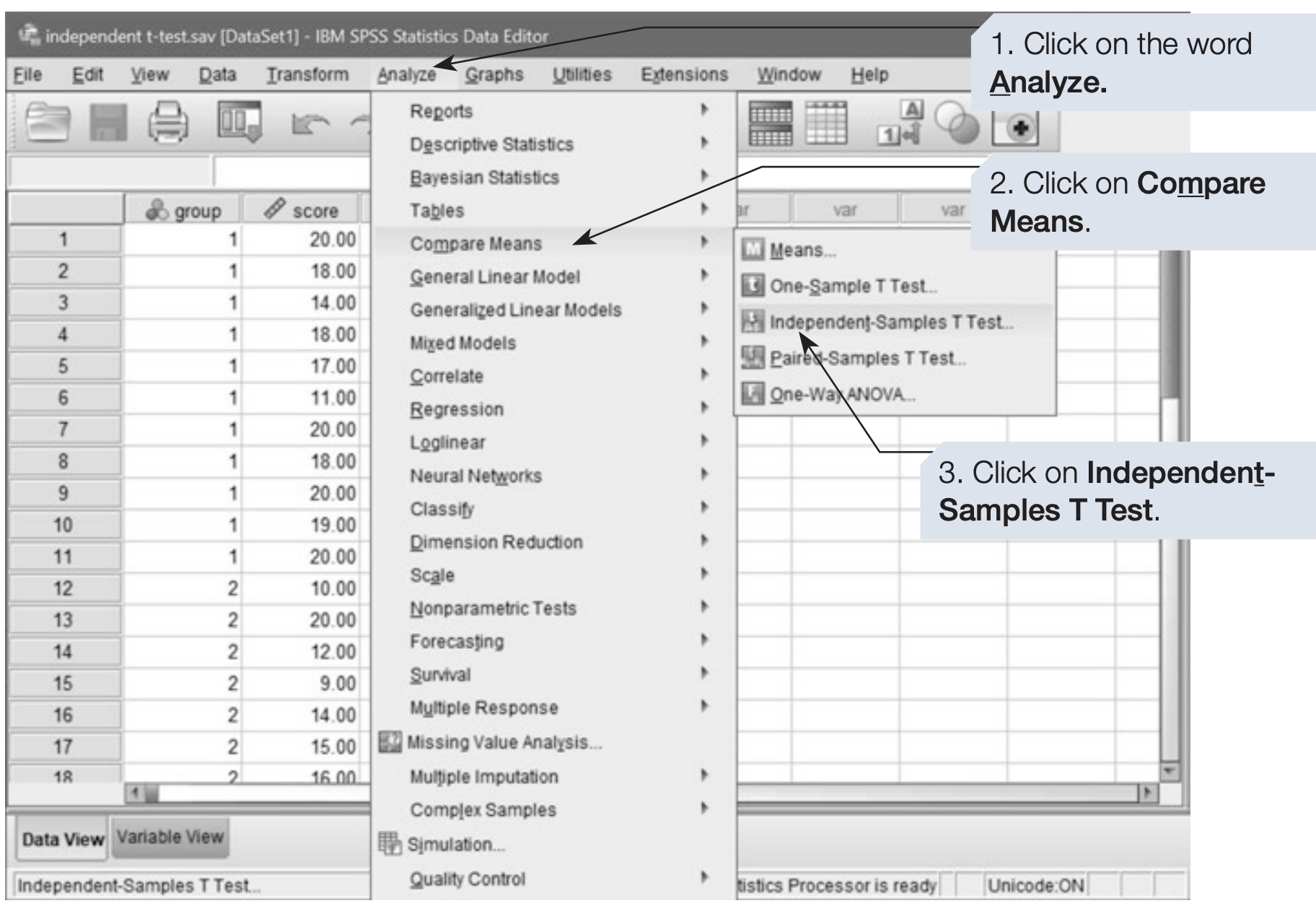
Performing a Indepeendent-Sample t-Test
SPSS Menu Path
Analyze → Compare Means → Independent-Samples T Test…
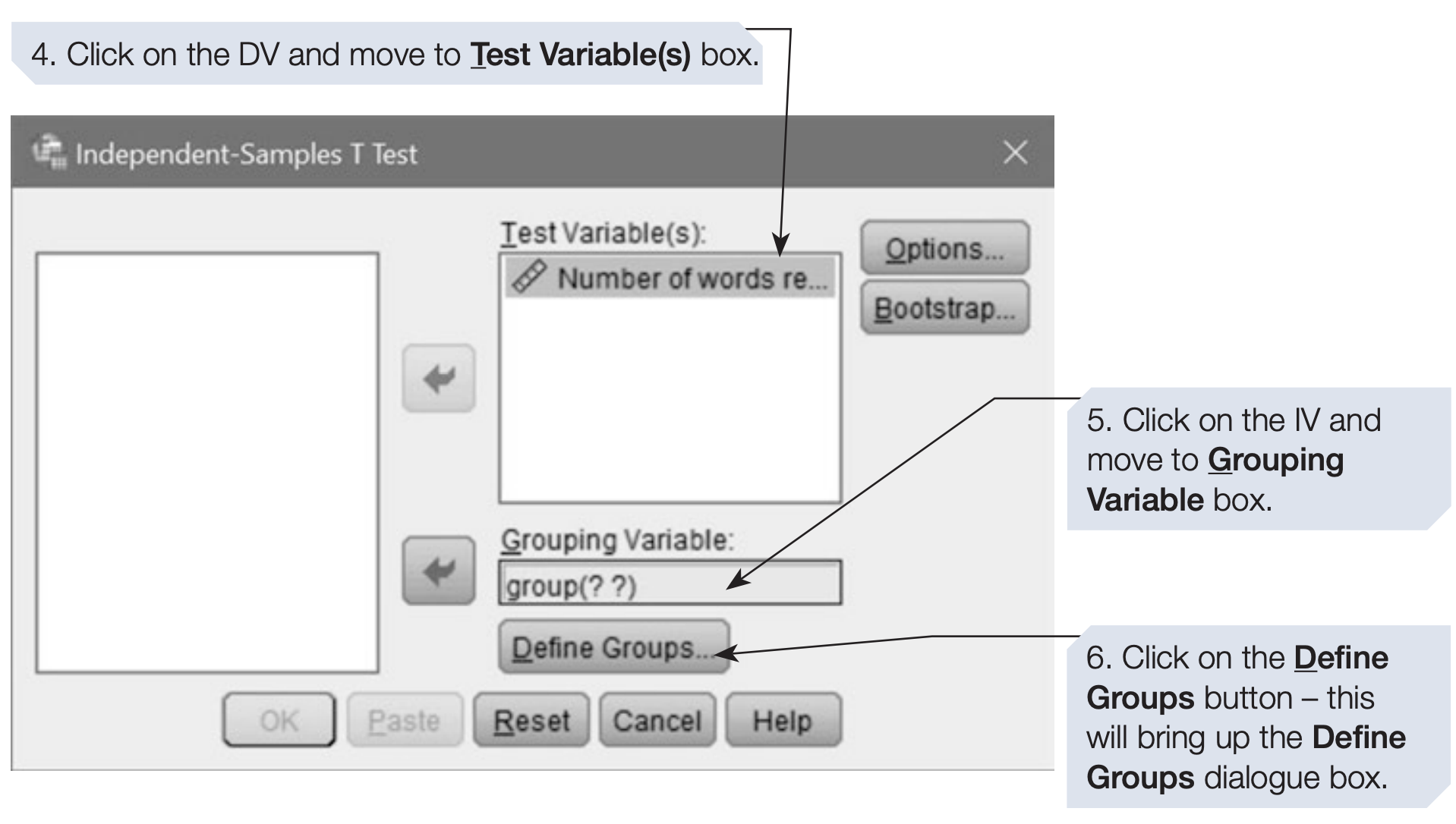
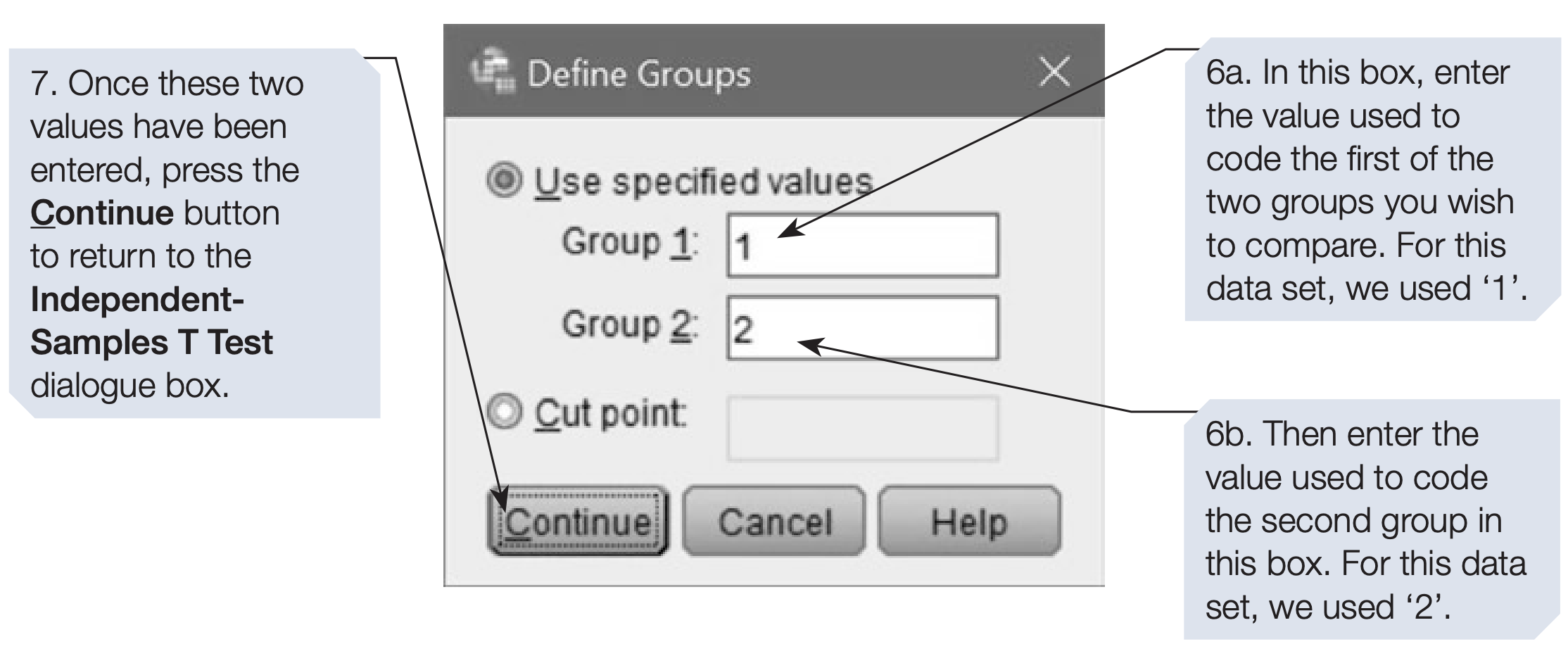
Group variable must be coded (e.g., 1 = Mnemonic, 2 = Non-mnemonic).SPSS Syntax
T-TEST GROUPS = Condition (1 2) /VARIABLES = MemoryScore /MISSING = ANALYSIS /CRITERIA = CI(.95).
SPSS Output
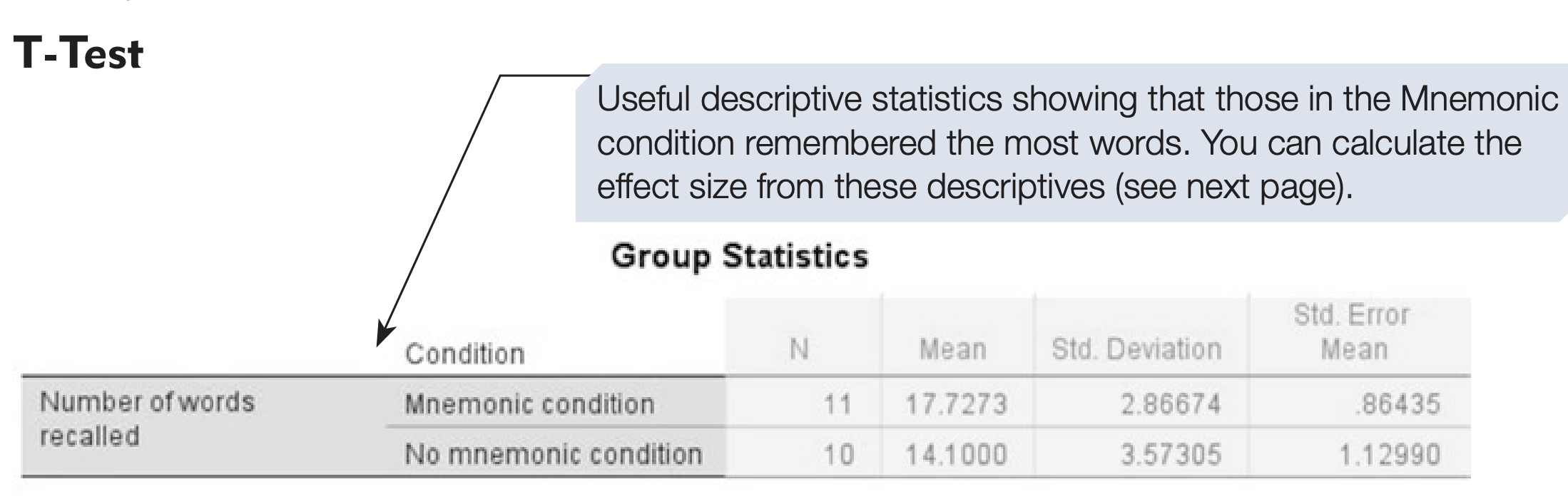
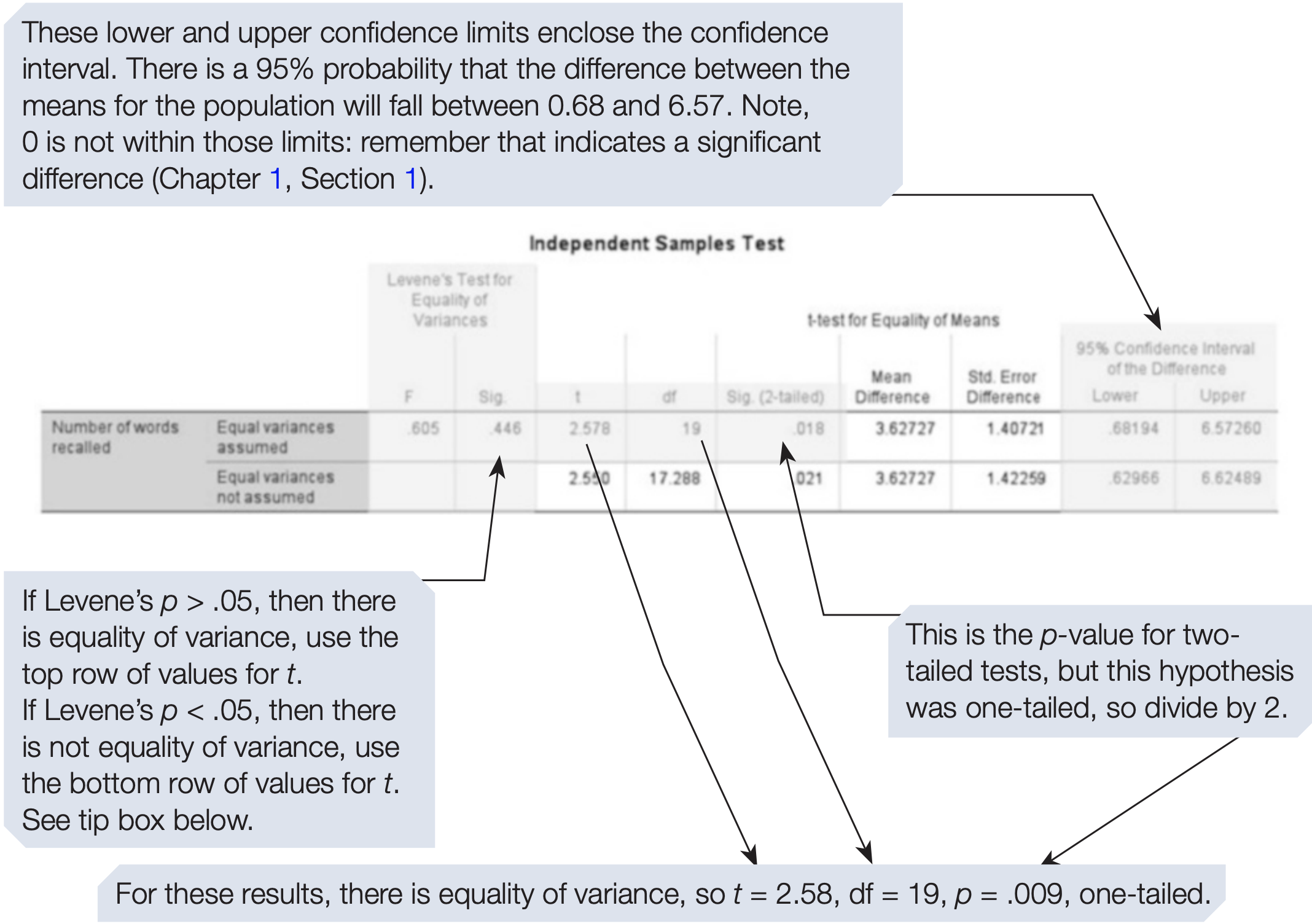
SPSS does not automatically provide an effect size for the independent t-test.
However, you can calculate this manually using Cohen’s d, which expresses the difference between means in standard deviation units (Fritz, Morris, & Richler, 2012):
\[ d = \frac{(x_1 - x_2)}{\text{mean } SD} \]
Use this formula when the group sizes (N) are approximately equal.
If the group sizes differ substantially, consult a statistics text for alternative methods of combining standard deviations.
Reporting the Results
Example write-up:
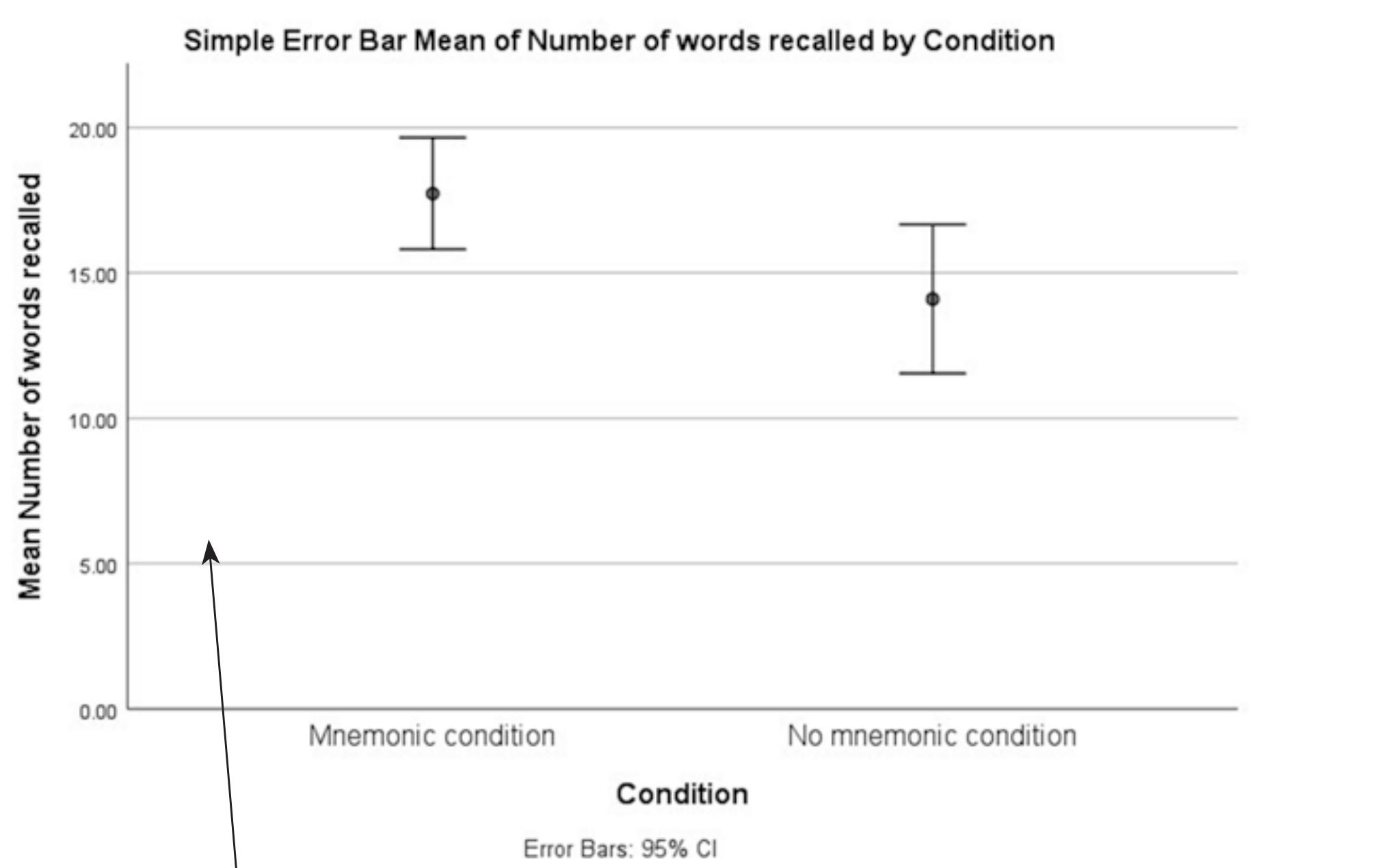
Participants in the Mnemonic condition recalled more words (\(M = 17.73\)) than those in the Non-mnemonic condition (\(M = 14.10\)).
An independent t-test showed this difference was significant (t = 2.58, df = 19, p = .009, one-tailed), with a large effect size (d = 1.13).
Creating an Error Bar Graph (Independent Groups Design)
In your report, it is good practice to include visual summaries of group differences.
SPSS can produce error bar graphs to show means and 95% confidence intervals.
For example, in the mnemonic memory study:
- The estimated population mean for the Mnemonic condition was 17.73, 95% CI [15.80, 19.65].
- The Non-mnemonic condition mean was 14.10, 95% CI [11.54, 16.66].
This visualisation provides a clear depiction of both central tendency and uncertainty.
To Create an Error Bar Graph in SPSS
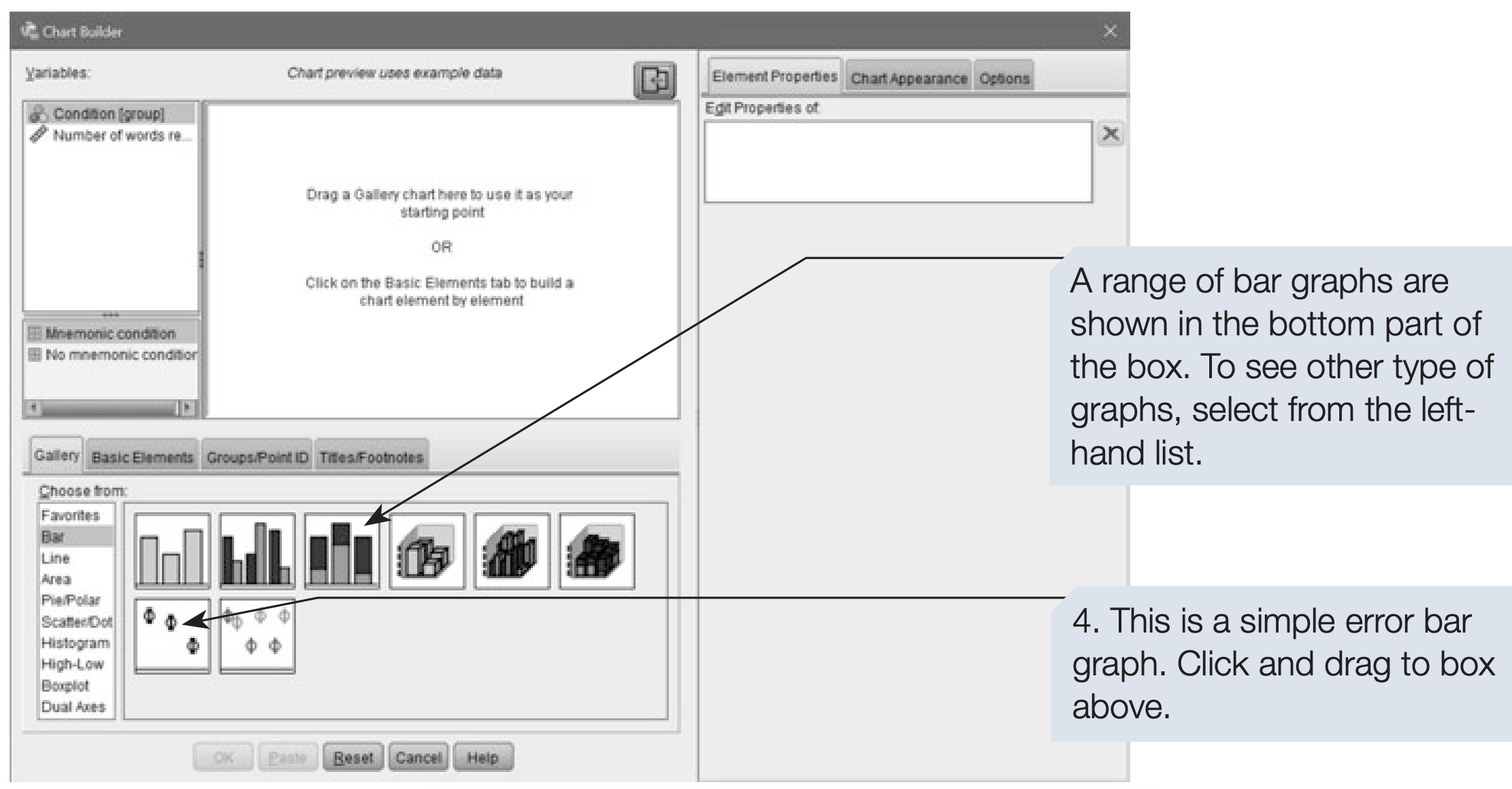
- From the menu, select Graphs → Chart Builder.
- Close the pop-up reminder about measurement levels.
- In the Chart Builder window, select the desired graph type and assign variables accordingly (see Chapter 3, Section 8 for details).
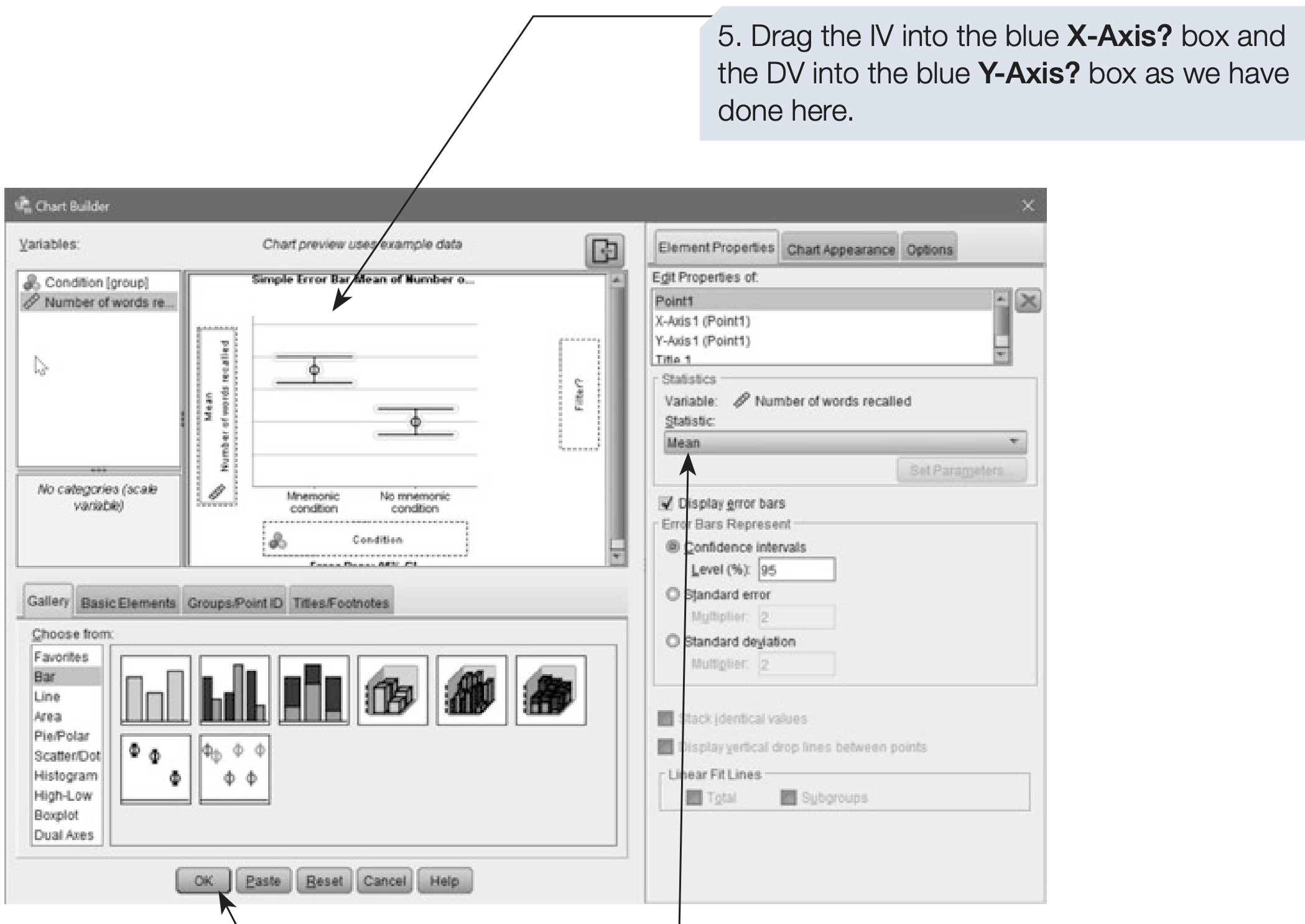

SPSS Output